Why does oscillation occur?

We've already discussed the reasons earlier.

The following diagram shows a MOS tube drive circuit with a series 10Ω resistor.

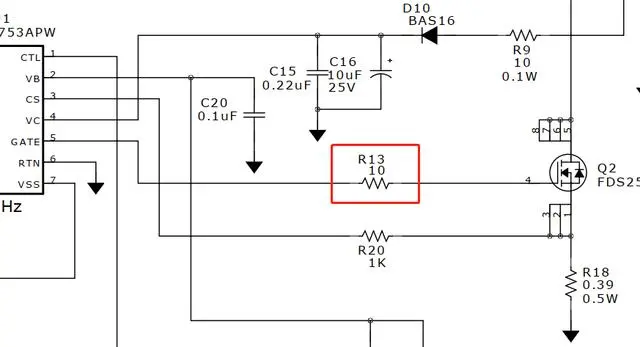
At first glance, it seems like there's no capacitor present, but there's parasitic inductance: the PCB has to route the lines from the driver chip to the MOS tube.

What about the capacitor? Power MOS tubes all have input capacitance, and the capacitance value isn't small.

When the left-side drive tube emits a switching signal, the internal resistance generally isn't very large. How large can this internal resistance be?

Let's assume a capacitance of 1nF, Rs=0.1Ω, RL=1MΩ:

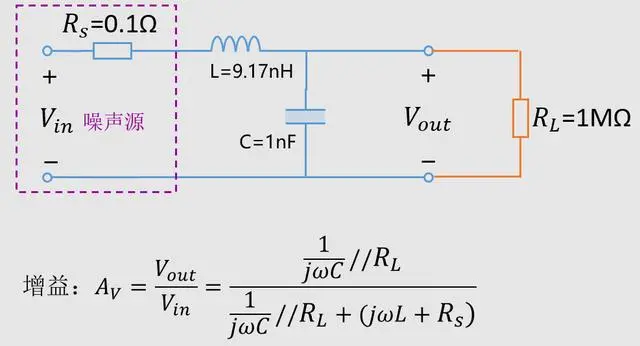
We know that the smaller the source internal resistance, the larger the load impedance, and the more likely it is to produce resonance peaks.

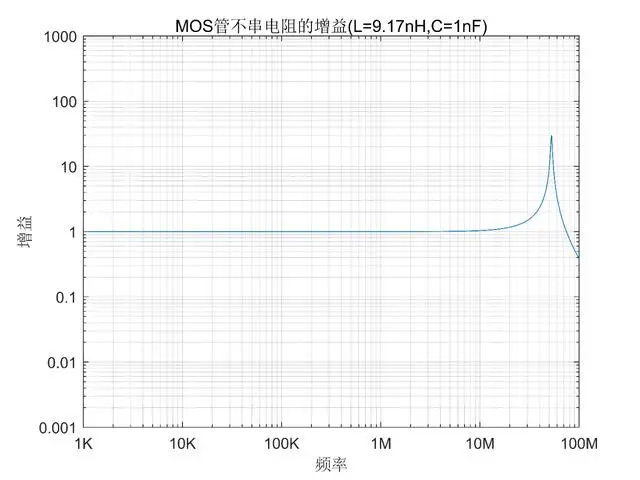
As shown in the diagram, at the resonance frequency of 52MHz, the gain reaches several tens of times. The MOS tube drive signal can be seen as a step signal, with a very rich frequency component. There are frequencies near 52MHz, so oscillation can occur.

Let's serially connect resistors of different values to see the difference, and these resistors can be equivalent to the internal resistance.

With resistors serially connected: 1Ω, 10Ω, 100Ω, it's equivalent to the circuit becoming Rs=1.1Ω, Rs=10.1Ω, Rs=100.1Ω, with other parameters unchanged.

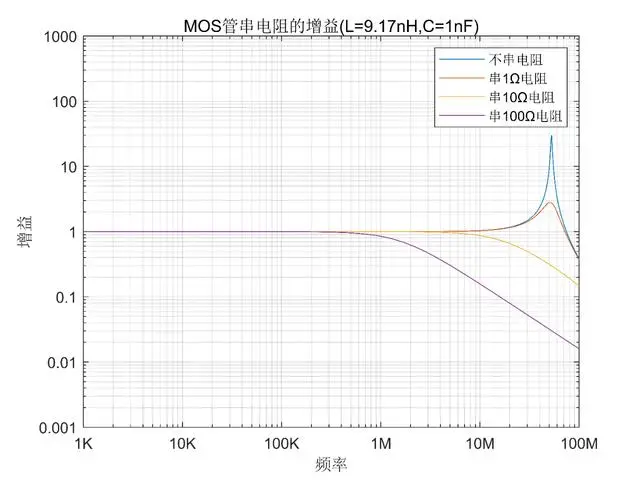
When a 1Ω resistor is serially connected: amplification, up to 3 times;

When a 10Ω resistor is serially connected: oscillation completely eliminated;

When a 100Ω resistor is serially connected: oscillation completely eliminated, but the cutoff frequency is lower, causing loss of high-frequency components in the drive signal, slowing down the rising edge, and lengthening the MOS tube's turn-on time.

The longer the G terminal wiring, the larger the parasitic inductance, and the more likely problems are to occur, so the resistance should be chosen larger.

In summary:

When a MOS tube is connected to a circuit, there's parasitic inductance generated by the leads, which, together with parasitic capacitance, can form a resonant circuit. For square wave waveforms, there are many frequencies present, so it's possible to match or approximate the resonance frequency, forming a series resonance circuit.

Adding a series resistor: effectively reduces the Q value of the resonant circuit, quickly attenuates oscillation, and avoids circuit malfunction.