Should we completely avoid LC series resonance? This detailed explanation is truly enlightening...

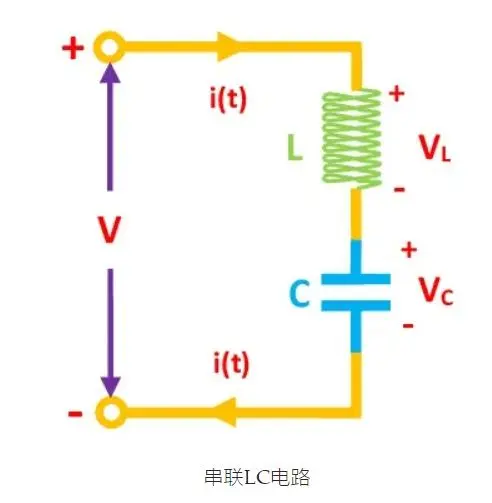
When an inductor and a capacitor are connected in series, resonance occurs at a specific frequency, which is known as the resonance frequency.

So, how does noise get amplified?

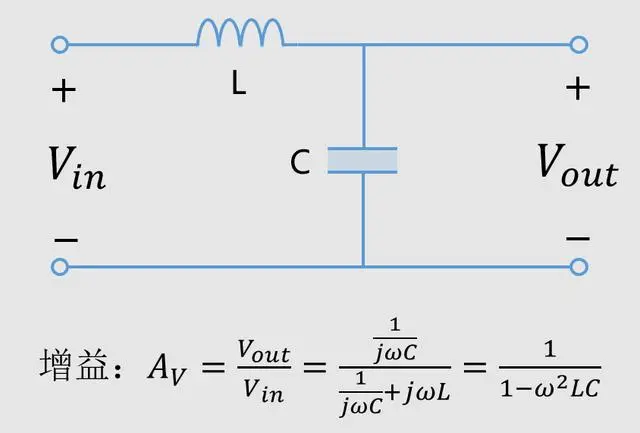
The gain, which is the ratio of output to input. If the gain is greater than 1, it means that the noise is amplified.

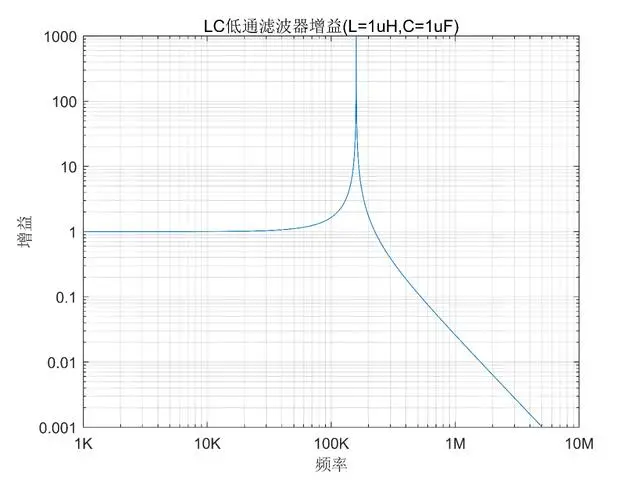
As shown above, the gain for a 1uH inductor and a 1uF capacitor.

At low frequencies, the gain is basically 1, meaning there is no amplification or attenuation.

At the resonance frequency, there is a very high peak.

In this ideal scenario, the peak is theoretically infinite, and the gain near the resonance frequency is extremely high.

As the frequency increases, the gain decreases, meaning the signal is attenuated.

If the gain at the resonance frequency can be reduced to around 0.7, then it functions as a very effective low-pass filter.

However, since inductors and capacitors are non-energy dissipative components, without the introduction of resistive components, the gain at the resonance frequency would be infinite.

Here's a question: Why does the effectiveness of LC filters sometimes worsen?

Because filter circuits need to be connected to a load, and after filtering the signal, it's connected to a load, causing the gain to change, as shown below: with added load.

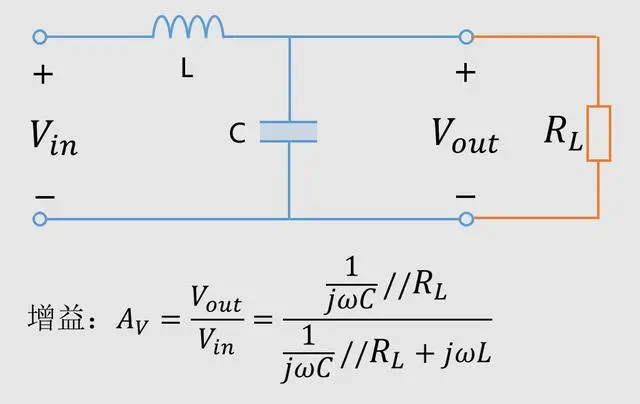
Gain curves with different RL after adding the load:

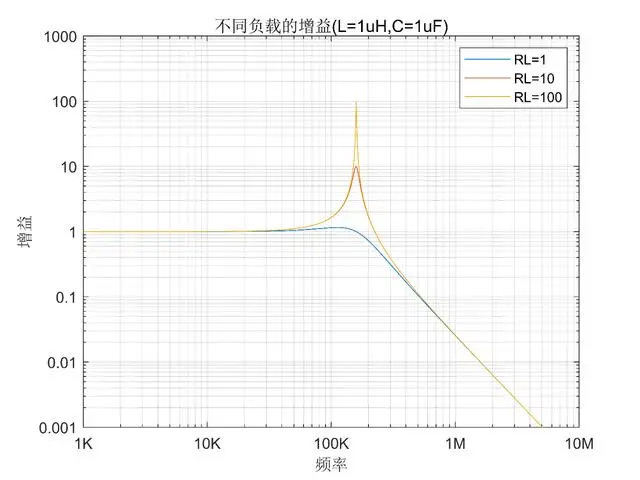
The smaller the load resistance, the smaller the gain at resonance, and the less likely noise amplification (caused by resonance) occurs.

In actual circuits, loads can be categorized as low impedance and high impedance. Generally, low impedance loads are less likely to result in poorer filter effects when connected.

Due to the different loads, the same LC filter may exhibit different effects when connected to different circuits, possibly better or worse.

Therefore, the lower the load impedance, the less likely it is to produce peaks.

In addition to the impact of load impedance, the internal resistance of the noise source also plays a significant role in resonance circuits.

In practical applications, noise models have a certain internal resistance.

(Based on different internal resistances, include internal resistance parameters)

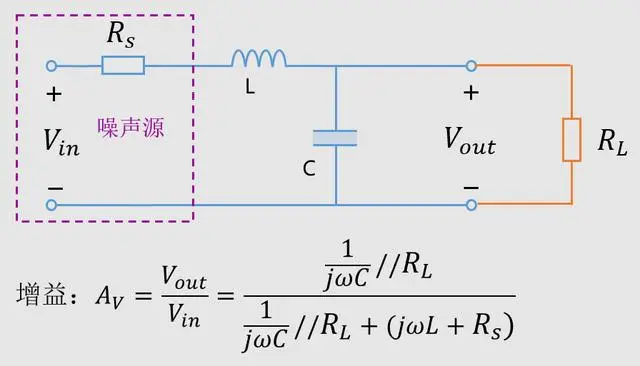
As shown in the figure, to eliminate the effect of load resistance, set it to a high impedance state: unified RL = 1MΩ, and analyze with different Rs.

It's concluded: the higher the internal resistance, the less likely it is to produce peaks, and vice versa.

Furthermore, the values of inductance and capacitance also have an impact, as shown below:

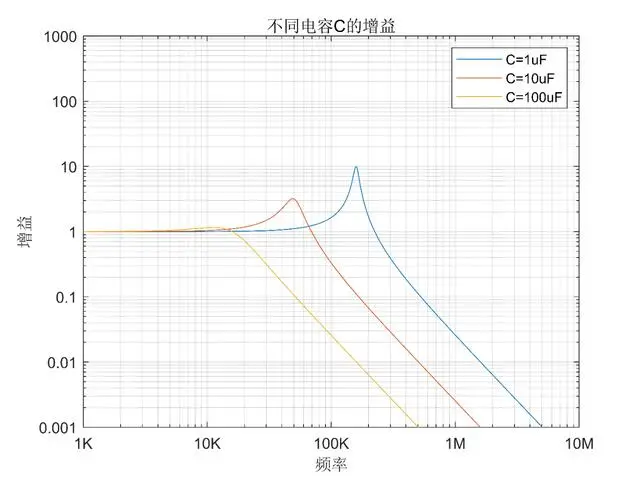
It's concluded: increasing capacitance reduces the peak.

In other words, when noise increases due to resonance, increasing capacitance can appropriately reduce noise.

However, note that when the peak decreases, it only means that the highest point has decreased, but it also causes a decrease in the resonance frequency, and the new resonance point may have a higher gain than before.

In other words, if noise happens to be in this frequency range, the effect after the change may become worse.

So what if we add a larger capacitor?

For example, adding a capacitor to 100uF. If the resonance points do not have an amplification effect, then basically the entire frequency band will not have an amplification effect.

The specific amount of capacitance to avoid the appearance of peaks actually has a certain relationship with the source resistance Rs, load impedance RL, and inductance L.

When the internal resistance RS increases from 0.1 to 1, the capacitance does not need to increase to 100uF. Keeping it at 1uF will also eliminate peaks.

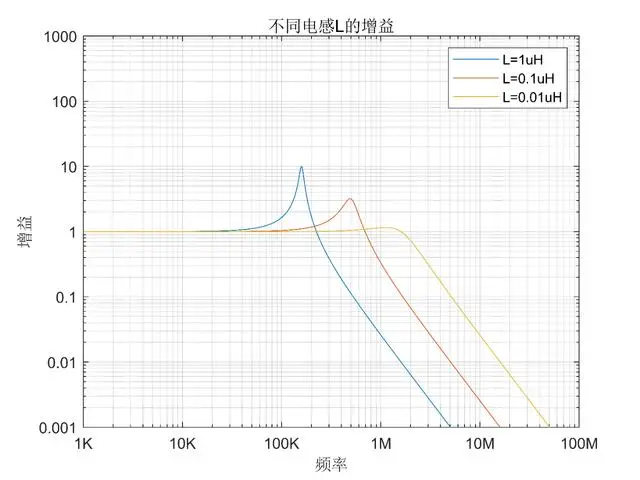
It's concluded: reducing inductance can reduce the height of the peak.

Therefore, for most circuits that want to reduce peaks, increasing capacitance or decreasing inductance can be used. If noise increases due to the use of an LC filter, increasing capacitance or reducing inductance can be considered.

Characteristics of series resonance circuits:

1. Impedance is resistive, with the minimum impedance and maximum current.

2. The voltage across the inductor and capacitor terminals reaches maximum.

With the above, in the next issue: How to suppress resonance with series resistance on the G terminal of a MOS tube?